概率统计

概率定义

有如下常用公式

$$\begin{aligned} & P(A\cup B)=P(A)+P(B)-P(AB) \\ & P(\overline{A}\overline{B})=P(\overline{A\cup B}) = 1-P(A\cup B) \end{aligned}$$

条件概率

条件概率公式

$$\begin{aligned} P(B|A)=\frac{P(AB)}{P(A)} \end{aligned}$$

经过变形，可以得到乘法公式

$$\begin{aligned} P(AB)=P(A)P(B|A) \end{aligned}$$

全概率公式

$$\begin{aligned} P(A)=P(B_1)P(A|B_1)+P(B_2)P(A|B_2)+...+P(B_n)P(A|B_n) \end{aligned}$$

独立事件

若两个事件相互独立，则

$$\begin{aligned} P(AB)=P(A)P(B) \end{aligned}$$

一维

泊松分布

是二项分布的极限

设$X\sim B(n,p)$，$\lambda = np$，则

$$\begin{aligned} & P(X=k)=e^{-\lambda}\frac{\lambda ^k}{k!} \\ & P(X \le n)=\sum^{n}_{k=0}e^{-\lambda}\frac{\lambda ^k}{k!} \end{aligned}$$

指数分布

概率密度函数为

$$f(x)=\left\{ \begin{aligned} \lambda e^{-\lambda x}, \quad x \gt 0\\ 0, \quad otherwise \end{aligned} \right.$$

分布函数为

$$\begin{aligned} F(x)=1-e^{-\lambda x} \end{aligned}$$

正态分布

定义

$$\begin{aligned} & f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \\ & X \sim N(\mu, \sigma^2) \end{aligned}$$

分布函数

标准正态分布的分布函数记为$\Phi(x)$，有表可查。

$$\begin{aligned} & F(x) = \Phi(\frac{x-\mu}{\sigma}) \\ & P(a \lt X \lt b) = F(b) - F(a) = \Phi(\frac{b-\mu}{\sigma}) - \Phi(\frac{a-\mu}{\sigma}) \\ & P(X \gt a) = 1 - F(a) = 1 - \Phi(\frac{a-\mu}{\sigma}) \\ & \Phi(-x)=1-\Phi(x) \end{aligned}$$

随机变量转换

已知$f_X(x)$和$Y=g(X)$，则$Y$的概率密度函数为

$$\begin{aligned} f_Y(y)=f_X[h(y)]|h'(y)|, \qquad \alpha \lt y \lt \beta \end{aligned}$$

其中$h(y)$是$g(x)$的反函数

二维

二维随机变量的分布函数为

$$\begin{aligned} F(x,y)=P(X\le x, Y\le y) \end{aligned}$$

离散型

独立性

若二维随机变量相互独立，则

$$P(X\le x, Y \le y)=P(X\le x)P(Y\le y)$$

即可以得到联合分布律与但变量分布律的关系

$$F(X,Y)=F_X(x)F_Y(y)$$

若$P(X=x_i , Y=y_j) = P(X=x_i)P(Y=y_j)$， 即$p_{ij} = p_{i.}p_{.j}$

连续型

独立性

1. 第一种方法

   $$\begin{aligned} & f(x,y)=f_X(x)f_Y(y) \end{aligned}$$

   另外由$f(x,y)=f_X(x)f_{Y|X}(y|x)$ ，可知若相互独立，则

   $$\begin{aligned} & f_Y(y)=f_{Y|X}(y|x) \\ & f_X(x)=f_{X|Y}(x|y) \end{aligned}$$

2. 第二种方法

   $$\begin{aligned} & f(x,y) = r(x)g(y) \\ & \operatorname{and:} \\ & f_X(x)=\frac{r(x)}{\int^{+\infin}_{-\infin}r(x)dx}=r(x)\int^{+\infin}_{-\infin}g(y)dy \\ & f_Y(y)=\frac{g(y)}{\int^{+\infin}_{-\infin}g(y)dy}=g(y)\int^{+\infin}_{-\infin}r(x)dx \end{aligned}$$

3. 推论

   若$U=u(x), V=v(x)$

   $$\begin{aligned} & F_{UV}(u,v) = F_U(u)F_V(v) \\ \end{aligned}$$

   举例来说，若$X,Y$相互独立，则$aX+b, cY+d$也相互独立

边缘分布律

二维随机变量$X,Y$关于某一分量的边缘分布函数指X或Y作为一元随机变量时的分布函数，

$$\begin{aligned} & F_X(x)=P(X\le x), F_Y(y)=P(Y \le y) \\ & F_X(x)=P(X\le x, Y \lt +\infin) = F(X, +\infin) \end{aligned}$$

不等式

• 马尔科夫不等式

$$\begin{aligned} P(|X| \ge a) \le \frac{E(|X|^k)}{a^k} \end{aligned}$$

数字特征

数学期望

离散型：

$$\begin{aligned} & P(X=x_k) = p_k, \qquad k=1,2,... \\ & E(X) = \sum^{+\infin}_{k=1}x_kp_k \\ & \operatorname{if} \quad Y=g(X): \\ & E(g(X)) = \sum^{+\infin}_{k=1}g(x_k)p_k \end{aligned}$$

连续性：

$$\begin{aligned} & E(X) = \int^{+\infin}_{-\infin}xf(x)dx \\ & \operatorname{if} \quad Y = g(X): \\ & E(g(X)) = \int^{+\infin}_{-\infin}g(x)f(x)dx \end{aligned}$$

二维连续型：

$$\begin{aligned} & E(X) = \int^{+\infin}_{-\infin} \int^{+\infin}_{-\infin}xf(x,y)dxdy \\ & E(Y) = \int^{+\infin}_{-\infin} \int^{+\infin}_{-\infin}yf(x,y)dxdy \\ & E(g(X,Y)) = \int^{+\infin}_{-\infin} \int^{+\infin}_{-\infin}g(x,y)f(x,y)dxdy \end{aligned}$$

常见数学期望表：

分布	期望
0-1分布	$p$
$B(n,p)$	$np$
$P(\lambda)$	$\lambda$
均匀分布	$\frac{a+b}{2}$
$E(\lambda)$	$\frac{1}{\lambda}$
$N(\mu, \sigma)$	$\mu$

性质：

$$\begin{aligned} & E(aX) = aE(x) \\ & E(X+Y) = E(X) + E(Y) \\ & E(\sum^n_{i=1}X_i)=\sum^n_{i=1}E(X_i) \\ \end{aligned}$$

如果X和Y相互独立

$$\begin{aligned} & E(XY) = E(X)E(Y) \end{aligned}$$

方差

概念

$D(X) = E((X-E(X))^2)$，即随机变量X的取值偏离平均值的平均偏离程度

离散型变量：

$$\begin{aligned} & P(X=x_k) = p_k, \quad k=1,2,... \\ & D(X) = \sum^{+\infin}_{k=1}(x_k - E(X))^2p_k \end{aligned}$$

连续型变量：

$$\begin{aligned} & D(X) = \int^{+\infin}_{-\infin}(x-E(X))^2f(x)dx \end{aligned}$$

常用公式

$$\begin{aligned} & D(X) = E(X^2) - E^2(X) \end{aligned}$$

常用方差表

分布	方差
0-1分布	$p(1-p)$
$B(n,p)$	$np(1-p)$
$P(\lambda)$	$\lambda$
均匀分布	$\frac{(b-a)^2}{12}$
$E(\lambda)$	$\frac{1}{\lambda^2}$
$N(\mu, \sigma)$	$\sigma^2$

性质

$$\begin{aligned} & D(aX) = a^2D(X) \\ & D(aX+b) = a^2D(X) \\ & D(aX\pm bY) = a^2D(X) + b^2D(Y) \pm 2abE((X-E(X))(Y-E(Y))) \\ & \qquad= D(X) + D(Y) \pm 2ab(E(XY)-E(X)E(Y)) \\ & \qquad= D(X) + D(Y) \pm 2ab\operatorname{cov}(X,Y) \end{aligned}$$

如果X和Y相互独立，则有

$$\begin{aligned} & D(X \pm Y) = D(X) + D(Y) \\ & D(\sum^n_{i=1}a_iX_i)=\sum^n_{i=1}D(a_iX_i)=\sum^n_{i=1}a_i^2D(X_i) \end{aligned}$$

协方差

定义

试图定义一种新的量，来反映随机变量$(X,Y)$之间的某种联系

$$\begin{aligned} \operatorname{cov}(X,Y)=E((X-E(X))(Y-E(Y))) = E(XY)-E(X)E(Y) \end{aligned}$$

相关系数：

$$\begin{aligned} \rho_{XY}=\frac{\operatorname{cov}(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}} \end{aligned}$$

若相关系数为0，则称$(X,Y)$不相关

性质

$$\begin{aligned} & \operatorname{cov}(aX, bY)=ab\operatorname{cov}(X,Y) \\ & \operatorname{cov}(X+Y, Z)=\operatorname{cov}(X,Z)+\operatorname{cov}(Y,Z) \end{aligned}$$

中心极限定理

对于随机分布序列$X_1, X_2, ..., X_n$，无论$X$服从什么分布，当n足够大时，$X_i$均服从正态分布

且对于$Y_n=Y(X_1,X_2,...X_n)$，有

$$\begin{aligned} & \frac{Y_n-E(Y_n)}{\sqrt{D(Y_n)}}\sim N(0,1) \\ & \lim_{n\rightarrow \infin}P(\frac{Y_n-E(Y_n)}{\sqrt{D(Y_n)}} \le y) = \Phi(y) \end{aligned}$$

注意$\sigma$是标准差，$\sigma^2$是方差

若对$\forall X_i, P(X_i=1)=p$，即服从0-1分布，那么

$$\begin{aligned} & Y_n = \sum^n_{i=1}X_i \sim B(n,p) \\ & Y_n \sim N(np, np(1-p)) \end{aligned}$$

统计量分布

常用统计量

样本均值

$$\begin{aligned} & \overline{X}=\frac{1}{n}\sum^n_{i=1}X_i \\ \end{aligned}$$

样本方差

$$\begin{aligned} & S^2=\frac{1}{n-1}\sum^n_{i=1}(X_i-\overline{X})^2 \\ \end{aligned}$$

k阶原点矩

$$\begin{aligned} & A_k=\frac{1}{n}\sum^n_{i=1}X_i^k \\ \end{aligned}$$

k阶中心矩

$$\begin{aligned} & B_k=\frac{1}{n}\sum^n_{i=1}(X_i-\overline{X})^k \end{aligned}$$

常用统计量有如下一些结论。设$E(X)=\mu, D(X)=\sigma^2$

$$\begin{aligned} & E(\overline{X})=\mu=E(X) \\ & D(\overline{X})=\frac{\sigma^2}{n}=\frac{D(X)}{n} \end{aligned}$$

另外，对于样本方差和2阶中心矩有如下结论：

$$\begin{aligned} & S^2=\frac{n}{n-1}S_n^2 \\ & S_n^2=\frac{1}{n}\sum^n_{i=1}(X_i-\overline X)^2 \\ & \quad =\frac{1}{n}\sum^n_{i=1}(X_i^2 - 2X_i \overline X + \overline X^2) \\ & \quad =\frac{1}{n}(\sum^n_{i=1}X_i^2 - 2\overline X\sum^n_{i=1}X_i + \sum^n_{i=1} \overline X^2) \\ & \quad =\frac{1}{n}(\sum^n_{i=1}X_i^2 - 2n\overline X^2 + n\overline X^2) \\ & \quad =\frac{1}{n}(\sum^n_{i=1}X_i^2 - n\overline X^2) \\ & \quad =\frac{1}{n}\sum^n_{i=1}X_i^2 - \overline X^2 \\ & \therefore E(S_n^2)=E(\frac{1}{n}\sum^n_{i=1}X_i^2) - E(\overline X^2) \\ & \qquad \qquad = \frac{1}{n}\sum^n_{i=1}E(X_i^2) - [D(\overline X) + E^2(\overline X)] \\ & \qquad \qquad = \frac{1}{n}\sum^n_{i=1}(\sigma^2 + \mu^2) - \frac{\sigma^2}{n} - \mu^2 \\ & \qquad \qquad = \sigma^2 + \mu^2 - \frac{\sigma^2}{n} - \mu^2 \\ & \qquad \qquad = \frac{n-1}{n}\sigma^2 \\ & \therefore E(S^2) = \frac{n}{n-1} \frac{n-1}{n}\sigma^2 = \sigma^2 \\ & \\ & D(S^2)=D[\frac{(n-1)S^2}{\sigma^2}\frac{\sigma^2}{n-1}] \\ & \qquad =(\frac{\sigma^2}{n-1})^2D(\frac{(n-1)S^2}{\sigma^2}) \\ & \qquad =(\frac{\sigma^2}{n-1})^2D(\chi^2(n-1)) \\ & \qquad =(\frac{\sigma^2}{n-1})^2(2n-2) \\ & \qquad = \frac{2\sigma^4}{n-1} \\ & D(S_n^2) = D(\frac{n-1}{n}S^2) \\ & \qquad = (\frac{n-1}{n})^2\frac{2\sigma^4}{n-1} \\ & \qquad =\frac{2(n-1)\sigma^4}{n^2} \end{aligned}$$

样本均值

若总体$X$服从正态分布$N(\mu, \sigma^2)$，那么从中抽取样本量为$n$的样本$X_1, X_2,...,X_n$的样本均值$\overline{X}$

$$\begin{aligned} & \overline{X}=\frac{1}{n}\sum^n_{i=1}X_i \end{aligned}$$

也服从正态分布，且

$$\begin{aligned} \overline{X} \sim N(\mu, \frac{\sigma^2}{n}) \end{aligned}$$

其他统计量的分布

• $\chi^2$分布

  若$X_1, X_2, ..., X_n$是来自正态总体$N(0,1)$的样本，则统计量$\chi^2$

  $$\begin{aligned} & \chi^2=\sum^n_{i=1}X_i^2 \\ & \chi^2 \sim \chi^2(n) \\ & E(\chi^2(n))=n, D(\chi^2(n))=2n \end{aligned}$$

  对于样本方差$S^2$，满足：

  $$\begin{aligned} & \frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1) \\ & \because S^2 = \frac{1}{n-1}\sum^n_{i=1}(X_i-\overline X)^2 \\ & \therefore \frac{1}{\sigma^2}\sum^n_{i=1}(X_i-\overline X)^2 \sim \chi^2(n-1) \end{aligned}$$

• $t$分布

  若$X\sim N(0,1), Y \sim \chi^2(n)$，$X,Y$相互独立，则统计量$T$

  $$\begin{aligned} & T = \frac{X}{\sqrt{Y/n}} \\ & T \sim t(n) \end{aligned}$$

• $F$分布

  若$X\sim \chi^2(m), Y\sim \chi^2(n)$，且$X,Y$相互独立，则统计量$F$

  $$\begin{aligned} & F=\frac{X/m}{Y/n} \\ & F \sim F(m,n) \end{aligned}$$

  $F(m,n)$的$\alpha$分位数$F_\alpha(m,n)$有表可查

  $$\begin{aligned} & P(F\le F_\alpha(n,m))=\alpha \\ & F_{1-\alpha}(n,m) = \frac{1}{F_\alpha}(m,n) \end{aligned}$$

点估计

矩估计法

即用样本矩来估计总体矩

求解过程：

$$\begin{aligned} & E(X) = \frac{1}{n}\sum^n_{i=1}X_i=\overline X \\ & E(X^2) = D(X) + E^2(X) = \frac{1}{n}\sum^n_{i=1}X_i^2 \end{aligned}$$

联立（1）（2）两式，其中$E(X)$，$E(X^2)$均用未知量表示，最终解得的结果是关于$\overline{X}$和$X_i$的函数

真搞懂啦~

极大似然估计法

• 求解过程：

  宗旨是让$L$尽可能大

  假设$X$符合的分布有与$\theta_1, \theta_2, ..., \theta_k$有关，$x_1, x_2, ..., x_n$是$X$的一组样本值

  1. 写出似然函数$L$

  2. 对$L$求的多个参数依次求偏导，一般来说可以对$\ln L$求偏导。

  $$\begin{aligned} & L(x_1, x_2, ..., x_n; \theta_1, \theta_2, ..., \theta_k) = \prod^n_{i=1}f(x_i;\theta_1,...,\theta_k) \\ & \frac{\partial}{\partial\theta_j}\ln L=0, \quad r=1,2,...,k \\ \end{aligned}$$

  3. 根据以上求得的极大似然估计值，求极大似然估计量，即用$X$替换$x$

     若$L$对于$\theta$不是可微的或偏导数=0无解，那么要考察$\theta$与$L$的相关性。

     若$\theta$越大$L$越大，则$\theta$取能取到的最大值

     若$\theta$越大$L$越小，则$\theta$取能取到的最小值

     或根据$f(x)$中$x$的范围确定$\theta$

• 不变性原理

  若$\hat\theta$是$\theta$的极大似然估计值，那么$\widehat{u(\theta)} = u(\hat\theta))$

点估计的评价方法

无偏性

对于总体参数$\theta$，若其估计量为$\hat\theta$，且

$$E(\hat\theta)=\theta$$

称$\hat\theta$是$\theta$的无偏估计量

• 主要运用数学期望的性质进行计算

有效性

设$\hat\theta_1$和$\hat\theta_2$都是总体参数$\theta$的估计量，若

$$\begin{aligned} D(\hat\theta_1) \lt D(\hat\theta_2) \end{aligned}$$

称$\hat\theta_1$比$\hat\theta_2$更有效

• 主要运用方差的性质进行计算
• 算数均值是所有线性无偏估计中方差最小的

一致性

也称“依概率收敛”，具体表示为：若当$n \rightarrow \infin$时，$\hat\theta \rightarrow \theta$，即

$$\begin{aligned} & \lim\limits_{x\rightarrow\infin}P\{\lvert\hat\theta - \theta\rvert\ge\epsilon\}=0 \end{aligned}$$

更常用的形式是

$$\begin{aligned} & \lim\limits_{x\rightarrow\infin}P\{\lvert\hat\theta - \theta\rvert\lt\epsilon\}=1 \end{aligned}$$

具体做题时，可借助切比雪夫不等式：

$$\begin{aligned} & P\{\lvert X-E(X)\rvert\lt\epsilon\} \ge 1-\frac{D(X)}{\epsilon^2} \end{aligned}$$

如果可证$\hat\theta$的无偏性，那么

$$\begin{aligned} & 1 \ge P\{\lvert\hat\theta-\theta\rvert\lt\epsilon\}\ge 1-\frac{D(X)}{\epsilon^2} \end{aligned}$$

在应用夹逼定理，即可证极限为1

区间估计

对于一个正态总体$X\sim N(\mu, \sigma^2)$

1. $\sigma^2$已知，$\mu$的置信区间，置信度$1-\alpha$

$$\begin{aligned} & Z=\frac{\overline{X}-\mu}{\sqrt{\frac{\sigma^2}{n}}} \sim N(0,1) \\ & \\ & P(\lvert Z \rvert \le z_{\frac{\alpha}{2}}) = 1-\alpha \\ & \\ & P(\overline{X}-z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}} \lt \mu \lt \overline{X}+z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}})=1-\alpha \end{aligned}$$

2. $\sigma^2$未知，$\mu$的置信区间

$$\begin{aligned} & T = \frac{\overline{X}-\mu}{\sqrt{\frac{S^2}{n}}} \sim T(n-1) \\ & \\ & P(\lvert T \rvert \le t_{\frac{\alpha}{2}}(n-1)) = 1-\alpha \\ & \\ & P(\overline{X}- t_{\frac{\alpha}{2}} (n-1) \frac{S}{\sqrt{n}}\lt \mu \lt \overline{X}+t_{\frac{\alpha}{2}}(n-1)\frac{S}{\sqrt{n}})=1-\alpha \end{aligned}$$

3. $\mu$已知，$\sigma^2$的置信区间

$$\begin{aligned} & Q=\sum^n_{i=1}(\frac{X_i-\mu}{\sigma})^2 \sim \chi^2(n) \\ & \\ & P(\chi^2_{\frac{\alpha}{2}}(n) \lt Q \lt \chi^2_{1-\frac{\alpha}{2}}(n)) = 1-\alpha\\ & \\ & P(\frac{\sum^n_{i=1}(X_i - \mu)^2}{\chi^2_{\frac{\alpha}{2}}(n)} \lt \sigma^2 \lt \frac{\sum^n_{i=1}(X_i - \mu)^2}{\chi^2_{1-\frac{\alpha}{2}}(n)})=1-\alpha \end{aligned}$$

1. $\mu$未知，$\sigma^2$的置信区间

$$\begin{aligned} & K=\frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1) \\ & \\ & P(\chi^2_{\frac{\alpha}{2}}(n-1) \lt K \lt \chi^2_{1-\frac{\alpha}{2}}(n-1))=1-\alpha \\ & \\ & P(\frac{(n-1)S^2}{\chi^2_{\frac{\alpha}{2}}(n-1)} \lt \sigma^2 \lt \frac{(n-1)S^2}{\chi^2_{1-\frac{\alpha}{2}}(n-1)})=1-\alpha \end{aligned}$$

假设检验

单个总体均值

$\alpha$的含义：$X-\mu_0$的值非常大（小），大到其发生的概率只有$\alpha$。$\alpha$通常只有0.05或0.01

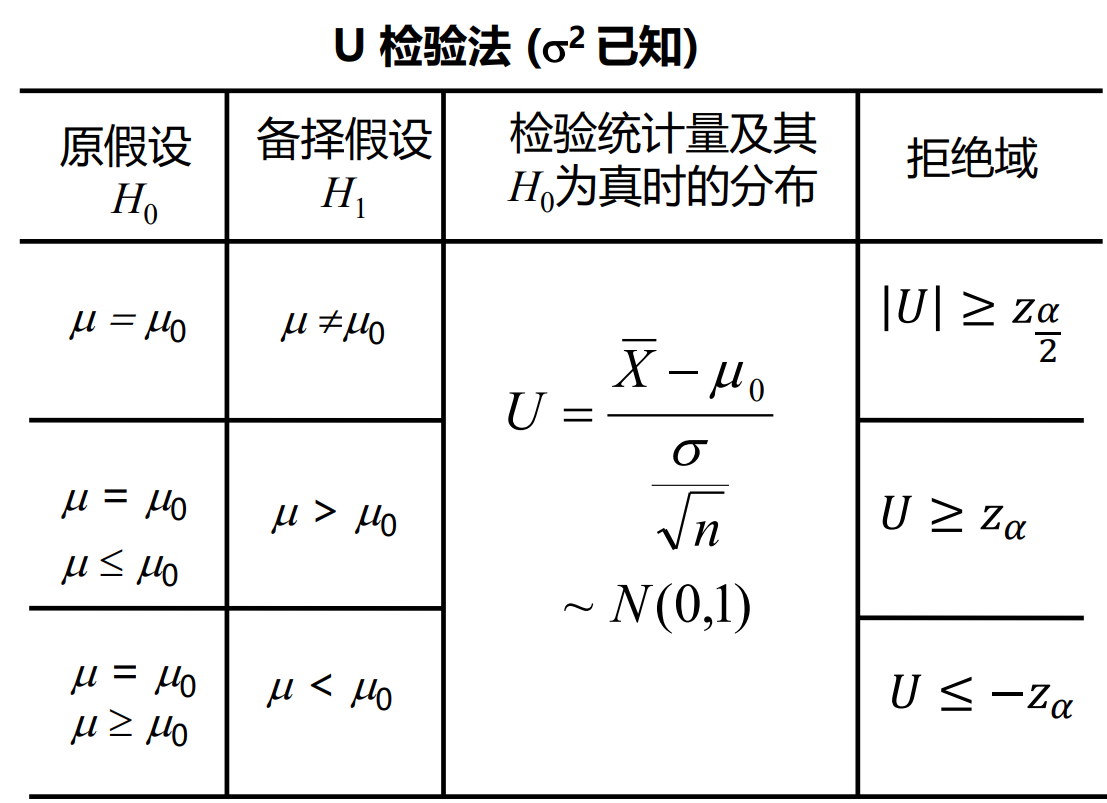
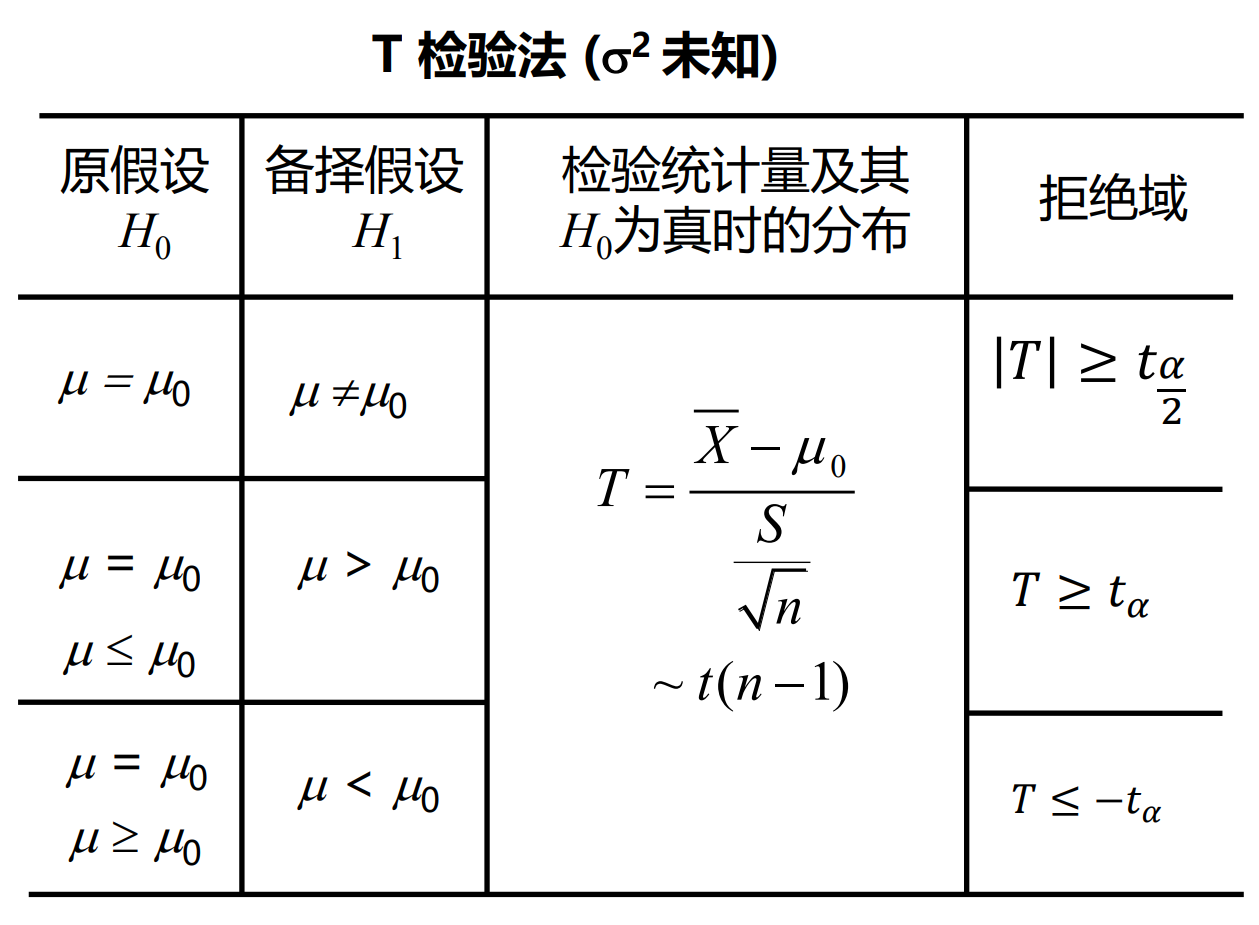
两个总体均值

设样本$X$有$n_1$个，$Y$有$n_2$个，且来自的总体的方差均为$\sigma^2$，那么检验统计量变为

$$\begin{aligned} t=\frac{\overline{X}-\overline{Y}}{S_w\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} \end{aligned}$$

其中$S_w^2$为两个总体方差的加权平均

$$\begin{aligned} S_w^2 = \frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2} \end{aligned}$$

拒绝与可参照上面两个表格

单个总体方差

$\frac{S^2}{\sigma_0^2}$非常大（小），大到其发生的概率只有$\alpha$。$\alpha$通常非常小，只有0.01或0.05

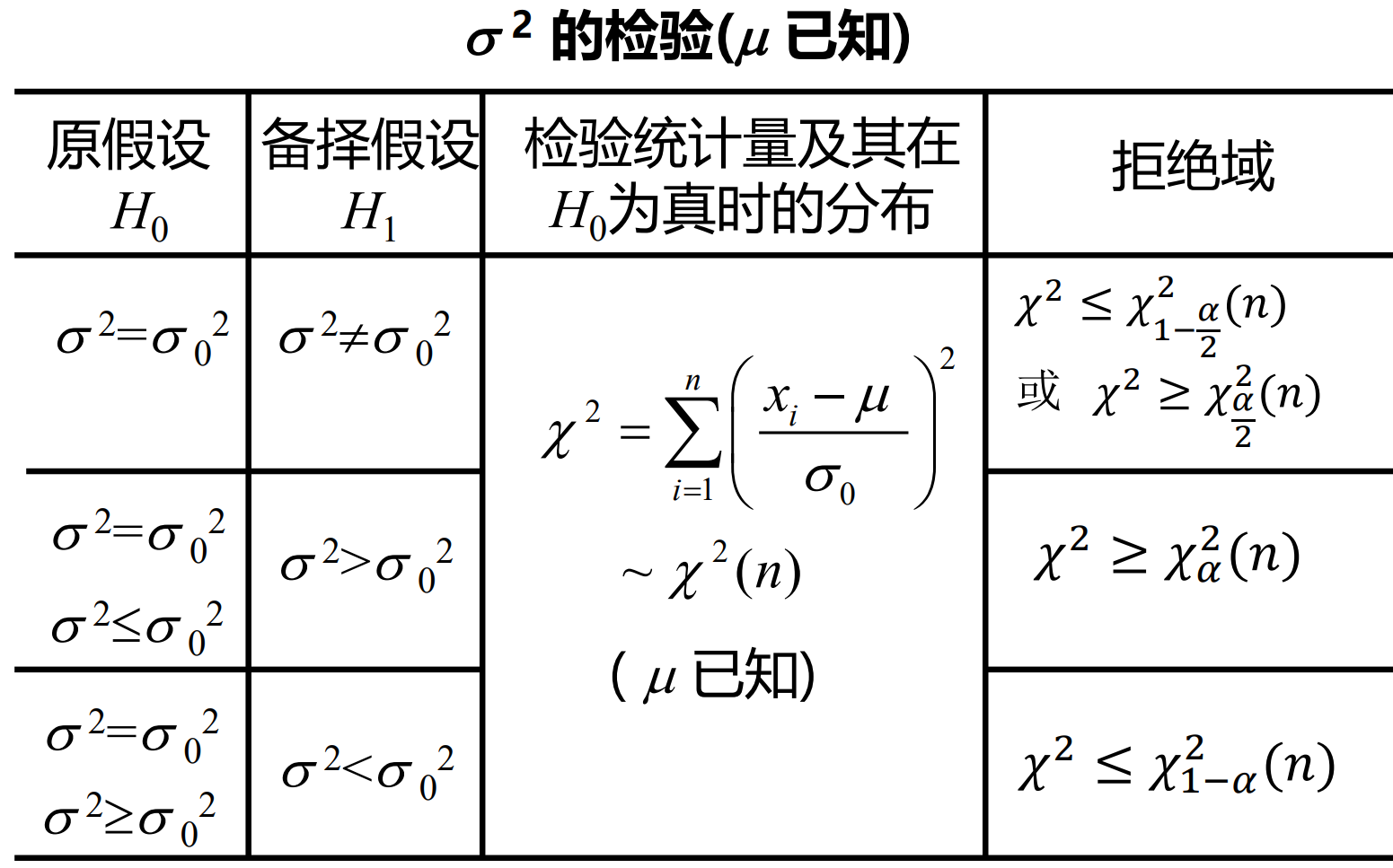
例题

1. 将4个可区分的球随机的放入4个盒子，求空盒子数量的数学期望

   设$X$为空盒子数量，$X_i$为第i个盒子是否为空。可得$X=X_1+X_2+X_3+X_4$。

   对于$X_i$，

   $$\begin{aligned} & P(X_i=1)=(\frac{3}{4})^4 \\ & P(X_i=0)=1-(\frac{3}{4})^4 \\ & \\ & \therefore E(X_i)=(\frac{3}{4})^4 \end{aligned}$$

   因此

   $$\begin{aligned} E(X)=E(\sum^4_{i=1}X_i)=\sum^4_{i=1}E(X_i)=4\times(\frac{3}{4})^4 \end{aligned}$$

   数学期望

2. 设在 [0, 1] 中随机地取两个数 $X , Y$ , 求$D(\min{X,Y})$

   要明确$\min{X,Y}$也是$g(X,Y)$的一种形式，因此应该先求出$(X,Y)$的联合分布律，在按计算$E(g(X,Y))$的方法进行计算

3. 相互独立与不相关

   若$X,Y$相互独立，则$P(X\lt x, Y\lt b)=P(X\lt x)P(Y\lt y)$

   若$X,Y$不相关，则$cov(X,Y)=0$

   在正态分布与特殊均匀分布中，独立等价于不相关